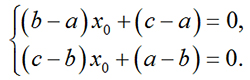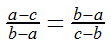Решение:
Нехай x
0 – спільний корінь трьох даних рівнянь. Тоді x
0 також є коренем рівняння, отриманого додаванням цих рівнянь:
(a + b + c)(x
3 + x + 1) = 0
Звідси випливає, що або x
03 + x
0 + 1 = 0, або a + b + c = 0.
Припустимо, що x
03 + x
0 + 1 = 0. Замінимо x
03 на -x
0 -1 першому та другому рівняннях умови:
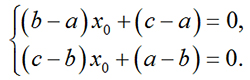
Отже,
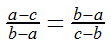
Ця рівність рівносильна рівності a
2 + b
2 + c
2 = ab + ac + bc, яка може бути перетворена до вигляду (a - b)
2 + (a - c)
2 + (b - c)
2 = 0
Але із останньої рівності випливає, що a = b = c. Протиріччя. Отже, a + b + c = 0. Можливі два випадки.
а) Одне із чисел дорівнює 0. Нехай, без обмеження спільності, c = 0 і a = -b > 0. Тоді рівняння ax
3 + bx + c = 0 має три корені x = 0, x = ±1.
б) Усі три числа відмінні від 0. Тоді знайдуться два одного знаку. Нехай, без обмеження спільності, a > 0, b > 0.
Тоді рівняння bx
3 + cx + a = 0 має корінь x = 1 і має корінь на проміжку (-∞,0) (оскільки при великих від’ємних x виконано bx
3 + cx + a < 0, а при x = 0 вірно bx
3 + cx + a = a > 0).