Задача 8.13

Відповідь: Доведення не має числової відповіді.

Перелік задач

Відповідь: Доведення не має числової відповіді.

Рішення:
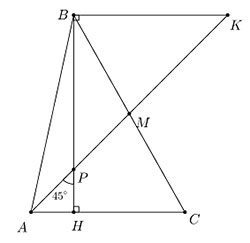
Нехай M – середина сторони BC, H – основа висоти, опущеної на сторону AC. Оскільки трикутник APH – прямокутний, то кут APH – гострий. Тоді саме він, а не суміжний з ним, дорівнює 45°.

Продовжимо медіану AM за точку M на її довжину, до точки K. Відмітимо, що трикутники AMC і KMB рівні за двома сторонами і кутом між ними.

Тому ∠KMB = ∠ACM. Отже, прямі AC і BK паралельні.

Оскільки пряма BP містить висоту трикутника ABC, опущену на сторону AC, то пряма BP перпендикулярна до прямої AC. Тоді пряма BP перпендикулярна також і до прямої BK, тобто ∠PBK=90°.

Оскільки ∠MPK = ∠APH = 45°, то PB = BK.

Але із рівності трикутників AMC і KMB випливає рівність відрізків AC і BK. Таким чином, PB = BK = AC.