Задача 8.9
Умова:Точка M – середина сторони AB трикутника ABC з кутом ∠ACB = 120°. На відрізках AC та BC вибрані відповідно точки P и Q такі, що AP = PQ = QB.
Знайдіть кут PMQ.
Знайдіть кут PMQ.
Підказка буде доступна через
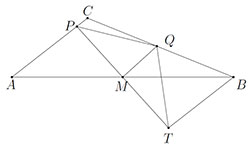Продовжимо відрізок PM на його довжину за точку M до точки T. Очевидно, трикутники APM и BTM рівні.
